In conjunction with Foresight Update 53
Recent results in SRMS
by J. Storrs Hall, PhD.
Research Fellow, Institute for Molecular Manufacturing
 |
| J. Storrs Hall, PhD |
In all the recent hullabaloo about “nanotechnology,” it has been largely forgotten that Drexler’s original vision of a revolutionary manufacturing technology rested on the ideas of two, not just one, of the 20th Century’s greatest thinkers. The one remembered, of course, is Feynman and his “Plenty of Room at the Bottom.” The other one was John von Neumann and his “Theory of Self-Reproducing Automata.”
I just had the privilege of reviewing the draft of a major new book by Rob Freitas and Ralph Merkle, which will likely become the classic reference in the subject. In his usual encyclopedic style, he organizes everything that is known about self-replicating systems.
While reviewing the book, I was bothered by an odd discrepancy. One of the standard architectures for a manufacturing system, proposed by Drexler, is convergent assembly. The idea is that you have a very large array of very small gadgets that make molecular-scale parts, and then an array of not-quite-as-small gadgets that put parts together into bigger parts, and so forth. At each stage the number of gadgets decreases by some fraction, and the size of the parts increases by some fraction.
One specific proposal, for example, by Merkle, is a cube which takes its inputs from 4 half-size (1/8 volume) cubes. The trick is that the half-size cubes run twice as fast as the big one — the product moves through them at the same absolute speed, and only has to go half as far. So the 4 small cubes feed 8 subassemblies to the big one for each time the big one spits out one object. Each small cube is in turn fed by 4 smaller cubes, and so forth.
To add a new stage, take four of your current system, and add a new cube of double the scale, increasing the total mass by 8. But you’ve only increased the output flow by 4. Thus the time the new system takes to produce its own mass in output is twice as long as the old one. This is called a one-third power scaling law of replication time to mass — i.e. replication time is proportional to the cube root of the mass.
| A single assembly module able to accept subassemblies from the four input ports to the right, and which produces a finished assembly to the left through the single output port. From “Convergent assembly” by Ralph Merkle, http://www.zyvex.com/nanotech/convergent.html | 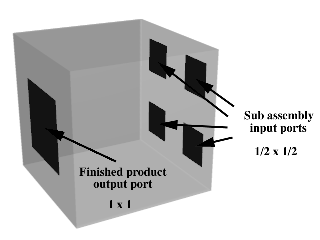 |
Any strictly self-similar convergent assembly system, that is, one in which each stage is a scale model of the next, and the same scale factor (and thus mass ratio) applies to all stages, must have a one-third power scaling law:
Consider a system with a branching factor of n, and working in units of the mass of a k-stage system and units of time to replicate a k-stage system:
Let x be the mass of the k+1st-stage node. The mass of the full k+1 stage system is then n+x. Thus the mass ratio of a k+1-stage system to a k-stage one is n+x. The output per unit time of a k+1-stage system is n, so the time to replicate for a k+1-stage system is (n+x)/n.
Lemma: The mass ratio of k+1-stage node to k-stage node is also n+x.
The ratio of head node to whole system is x/(n+x), which equals the ratio of k-stage node to the whole subsystem it is the head of, but since that is 1 by definition, the mass of a k-stage node is just x/(n+x). Thus ratio of k+1-stage node to k-stage node is x/(x/n+x), which equals n+x, qed.
Now for a scaling law of 1/z power, time to replicate to the power z equals mass ratio, i.e.
((n+x)/n)z = n+x
(n+x)(z-1)/nz = 1
(n+x)(z-1) = nz
n+x = n(z/(z-1))
x = n(z/(z-1)) – n
and therefore n+x = n(z/(z-1))
Because of strict scaling, the area of the output port on any node scales with the area of a side, and since the flow of material out of a node must equal the total flow into it,
(n+x)(2/3) = n
Thus z must equal 3 for any strictly self-similar convergent assembly system, i.e. such systems must have a one-third power scaling law.
So what’s the discrepancy? It turns out that natural systems, like animals and plants, empirically have a well-documented one-fourth power scaling law, not only for time to reproduce but for a number of other properties like metabolic rate. In other words, if you increase system mass by a factor of 1000, replication time goes up by 5.62 rather than 10. There’s a series of papers by West, Brown, and Enquist of the Santa Fe Institute explaining how this is related to the fractal nature of vascular (and similar) systems.
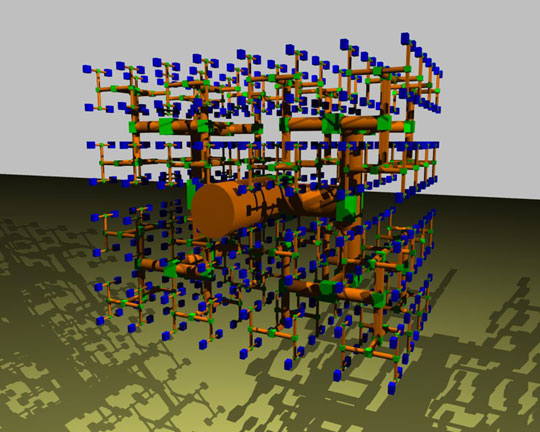 |
| Geometry for a convergent-assembly system with a one-fourth power scaling law. |
It’s not just fractalness, however — I worked out the above proof to show that there’s something more going on (and tease out just what it was). To achieve a 1/4-power law, we must relax the scaling a tiny bit: we allow the length of units to scale by one factor (l), and the radius (= the other two dimensions) to scale by a different one (r).
Now the mass ratio is l*r2 = n+x. z=4 implies n+x = n(4/3). Fixed output area implies r2 = n, and therefore
l = (n+x)/r2 = n(4/3)/n = n(1/3)
The simplest design following the new rules is to let n (the branching factor) equal 2, so we have a binary tree structure, with l equal the cube root of 2, and r equal the square root of 2.
The design is a fractal plumbing embedded in a box that is 1 by 2(1/3) by 2(2/3). We can recursively divide the box in half, running a pipe in from the center of a large side and slicing to halve the long dimension, giving two boxes similar to the first one. The pipes decrease in length by 2(-1/3) (0.7937), and in radius by 2(-1/2) (0.7071).
It remains to be seen of course, whether we can design actual assembly machinery along these lines!
References:
http://www.santafe.edu/sfi/research/focus/networkDynamics/projects/scalingNetworks.html
http://www.zyvex.com/nanotech/convergent.html
—Dr. J. Storrs Hall is an IMM Research Fellow. He can be reached at josh@imm.org.
IMM would appreciate learning your thoughts on the above article.
